Animation for some figure-eight solutions under Lennard-Jones potential

See also Hiroshi Fukuda's site ``Three Body Problem'' http://kilin.clas.kitasato-u.ac.jp/3body/

Hiroshi Fukuda found many figure-eight solutions under Lennard-Jones potentail U=1/r^{12}-1/r^6.
The preprint
[1] H. Fukuda, T. Fujiwara and H. Ozaki, Figure-eight choreographies of the equal mass three-body problem with Lennard-Jones-type potentials, http://arxiv.org/abs/1606.08760
You can see many series for figure-eights in this paper.

The existence of figure-eight solutions under Lennard-Jones potential was predicted by L. Sbano in his talk at SPT 2004 held at Cala Gonone, Italy. He predicted that ``there are at least two solutions for sufficiently large period''.
[2] L. Sbano, Symmetric solutions in molecular potentials, Proceedings of the international conference SPT 2004, World Scientific, 2005
[3] L. Sbano and J. Southall, Periodic solutions of the N-body problem with Lennard-Jones type potentials, Warwick preprint, June 2007
[4] L. Sbano and J. Southall, Periodic solutions of the N-body problem with Lennard-Jones type potentials, Dynamical Systems Vol. 25 #1, 2010

The followings are animations for some figure-eights that are found by Hiroshi Fukuda.

• Animation 1: (x_0, y_0, E)=(1.5, 1.427721000, 0.000122434)
  T=341.278
  
  The three black points represent the position of q_k, k=0, 1, 2. As you see in the movies, the three bodies bounce as if they were balls with radious r_0=2^{1/6}/2=1.122... that are represented by circles. Two bodies feel repulsive force, when the distance between them is smaller than 2 r_0=2^{1/6}. Otherwise, they feel attractive force. See the following figures for U(r), repulsive case, and attractive case.
  

  ---

• Animation 2: (x_0, y_0, E)=(0.75, 0.64808093, -0.14752617)
  T=44.485
  

  ---

• Animation 3: (x_0, y_0, E)=( 0.473207906706962783102256117707, 1.01061071815628640266937160262, -0.2)
  T=111.029
  

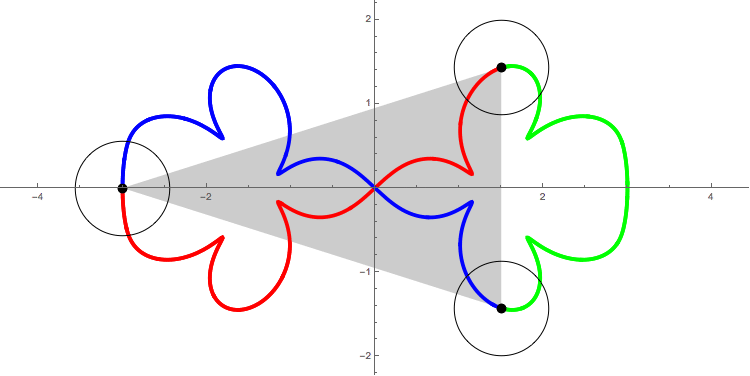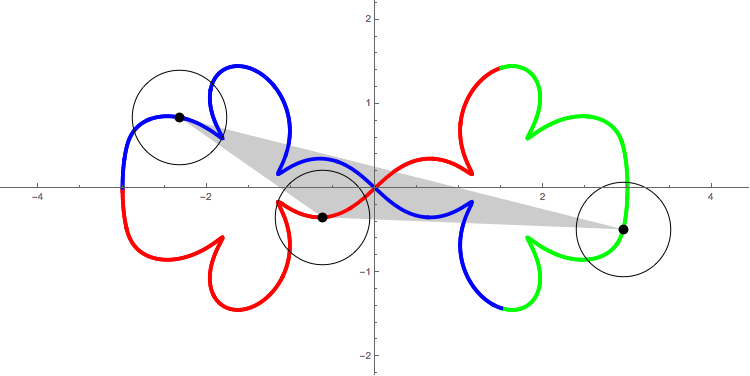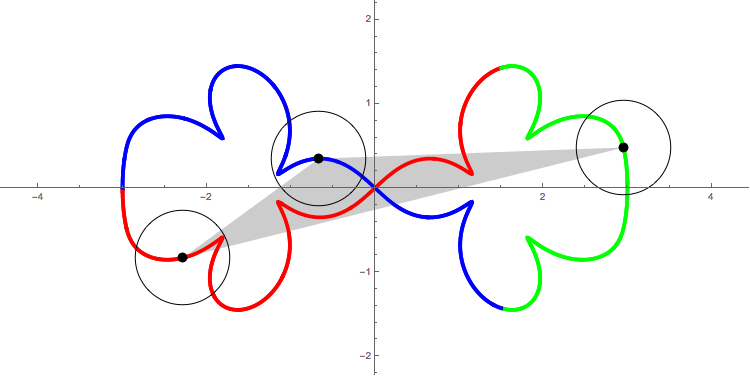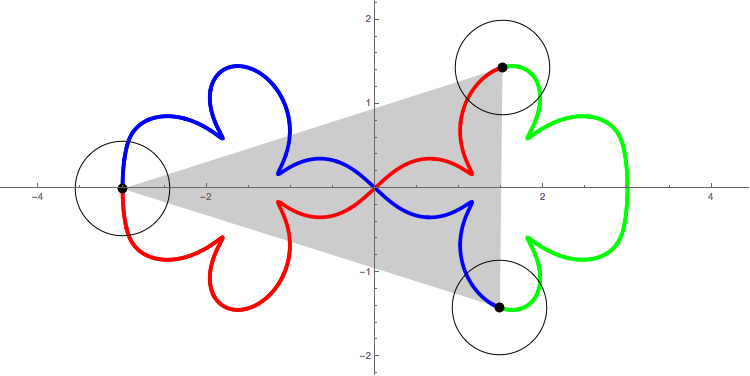
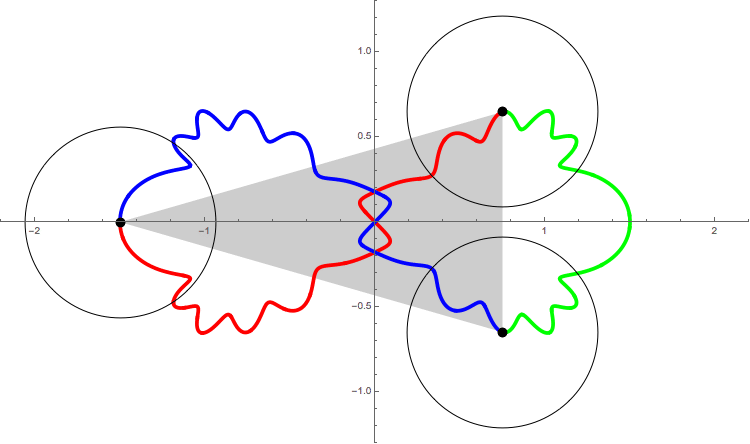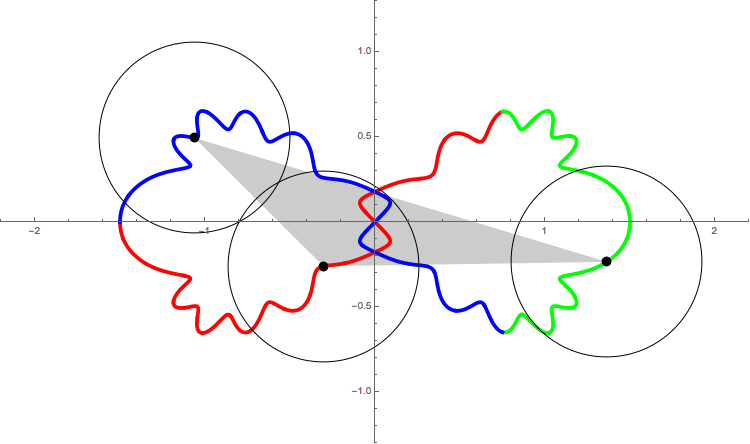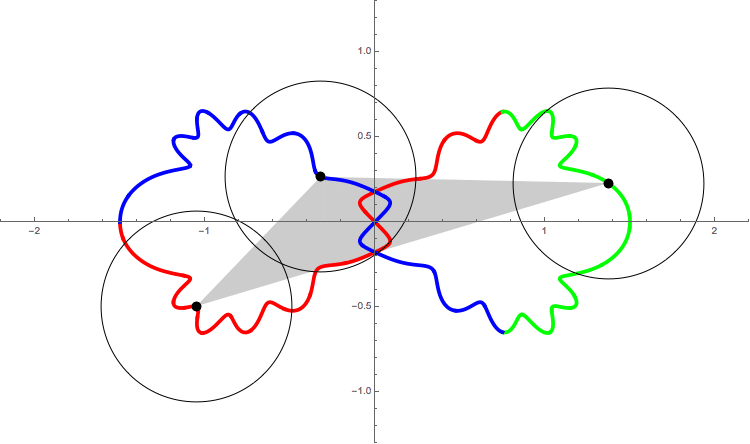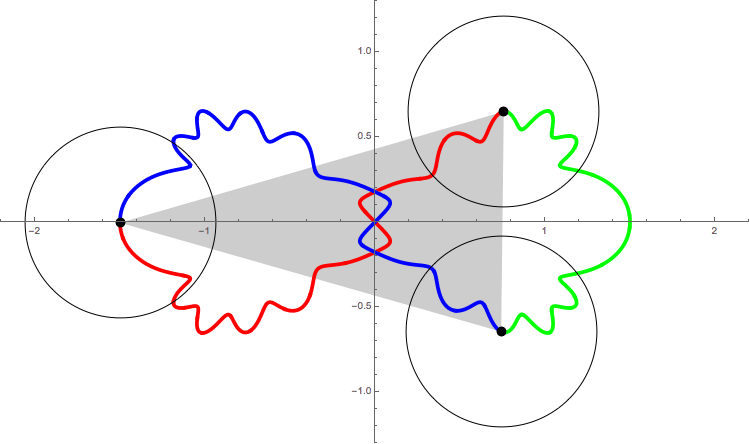
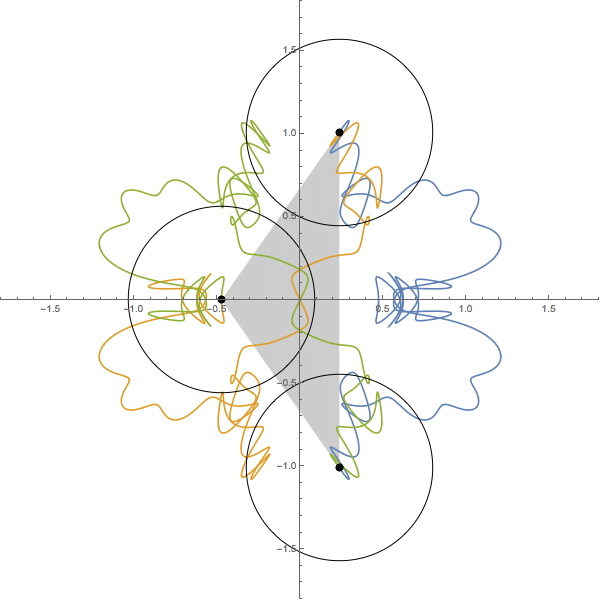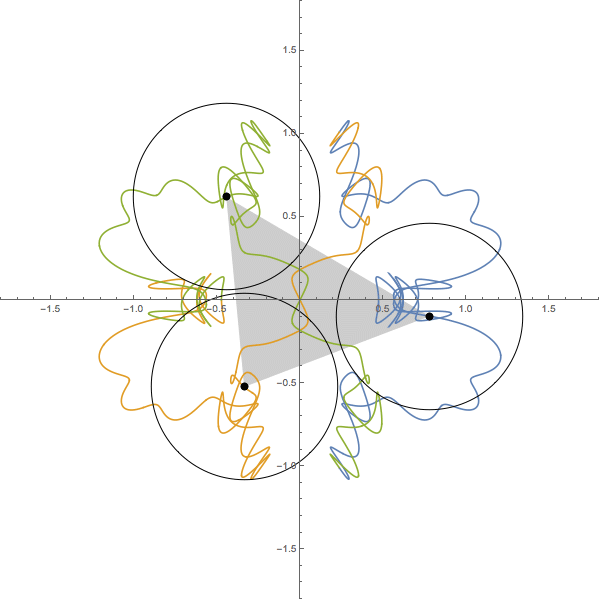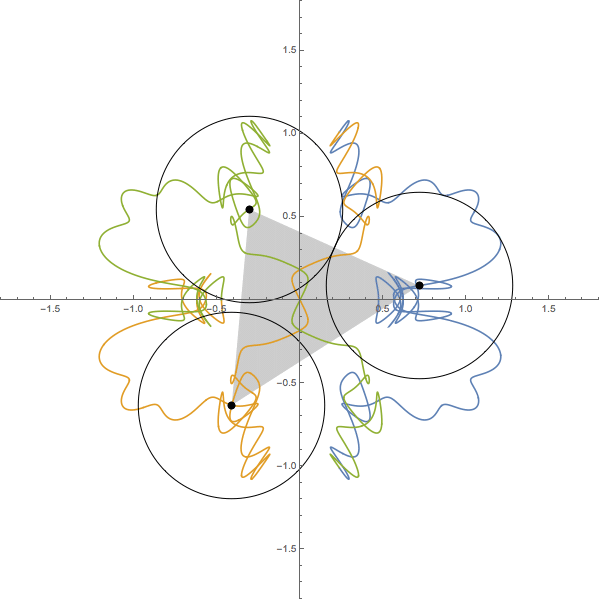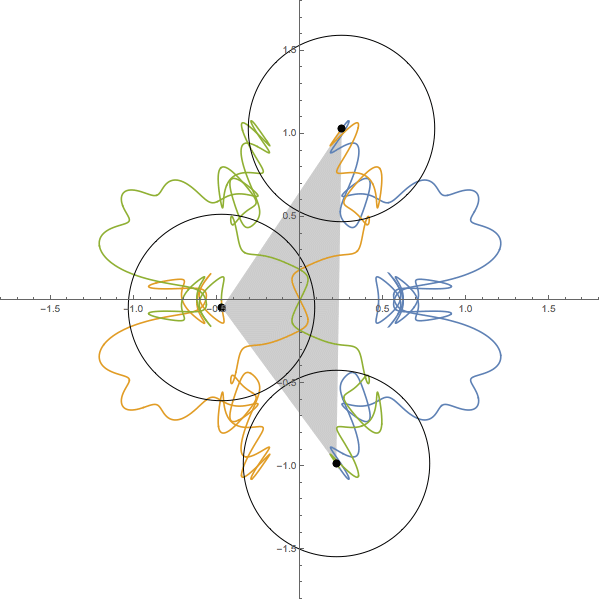
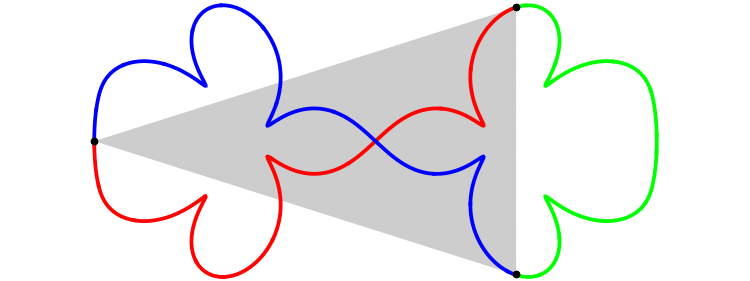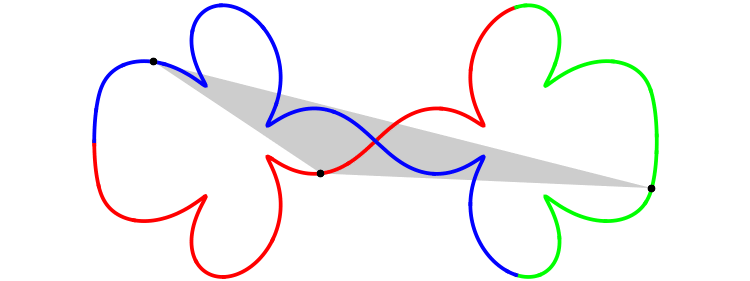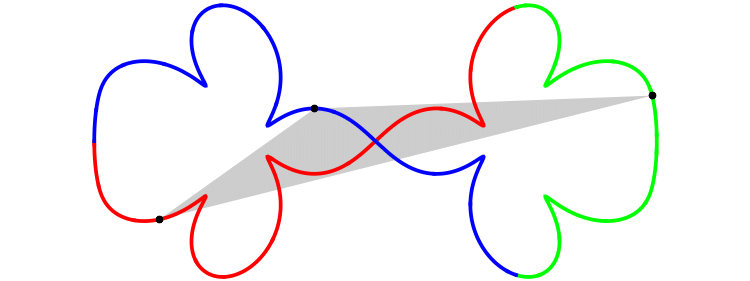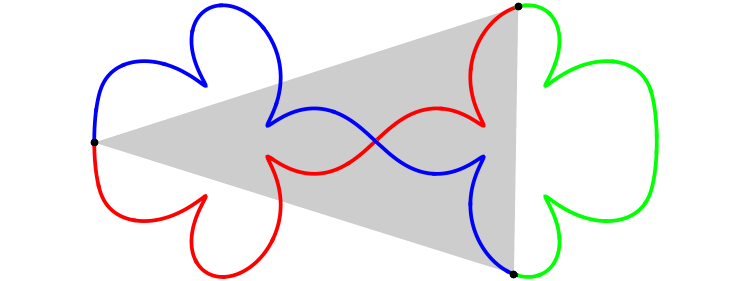
The following figure shows the orbit of the figure-eight of animation 3 in the ``shape plane'', q_3(t)/(q_2(t)-q_1(t)).

If you need more precise picture, follow this link 20160703LennardJonesFig3Shape3.pdf

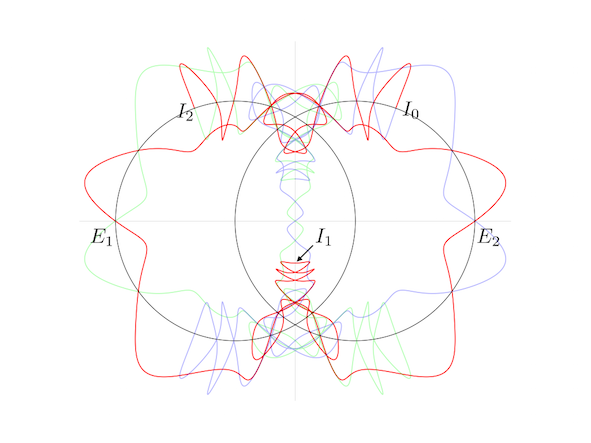
The X-axis is the equator of the ``shape sphere''. Any points on the equator represents colinear configuration. The Y-axis and two circles are the lines of longitude of the ``shape sphere'', whose mutual angle is equal to 2\pi/6. Any point on these five longitude lines represents isosceles configuration.

The red curve represents the interval of time [0, T/3]. And green and blue one represent [T/3, 2T/3] and [2T/3, T] respectively.

See the red curve.
At t=0, the motion starts at the isosceles configuration I_0. At t=T/12, it passes through the Euler point E_1. Then at 2T/12, I_1. Namely, in short expression, I_0(t=0) --> E_1(T/12) -->I_1(2T/12) --> E_2(3T/12) --> I_2(4T/12=T/3)

In the interval of time [0, T/3], the motion passes through just two Euler points E_1 and E_2. For isosceles configurations, although the motion passes through many isosceles configurations, only pathes at I_0, I_1 and I_2 are parpendiculer to the longitude line. This is the requirement for the figure-eight solution. So, this solution has a qualification to be called ``one of the figure-eight solution''.