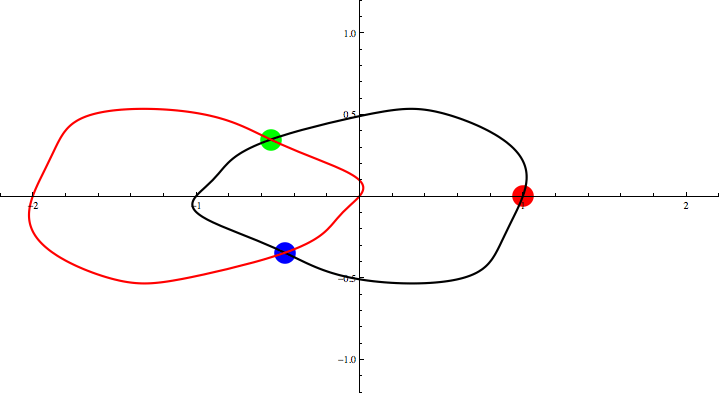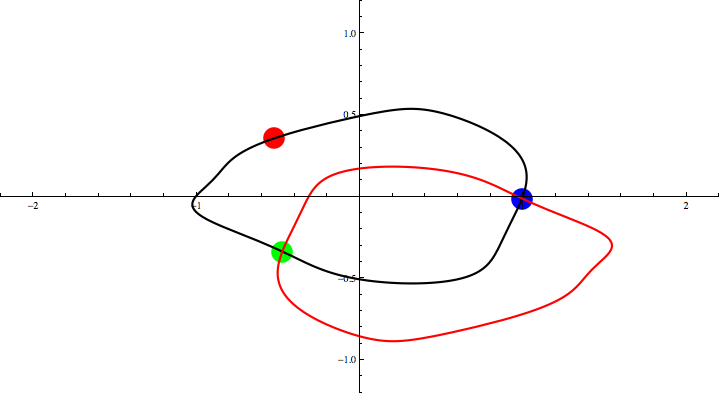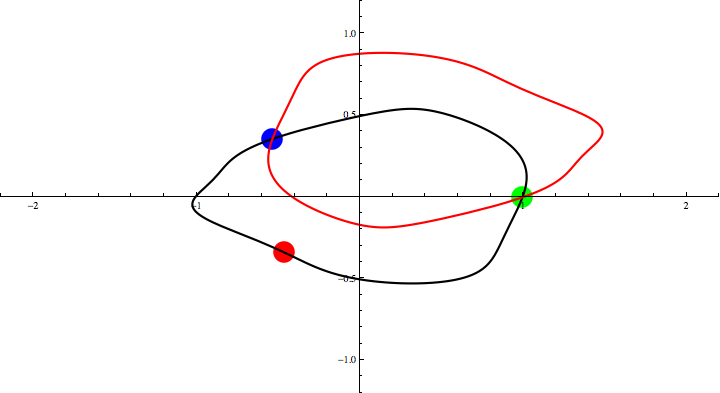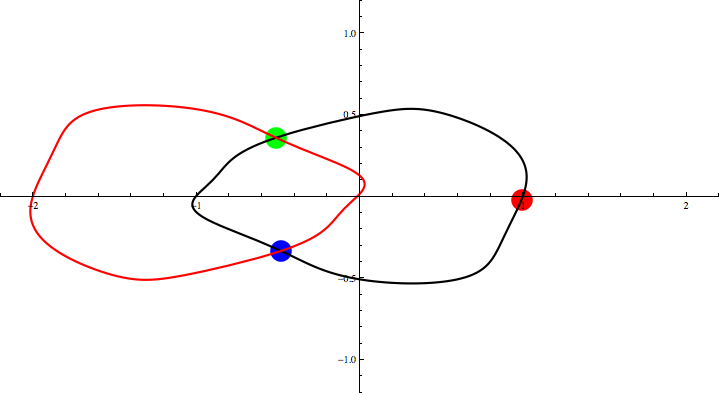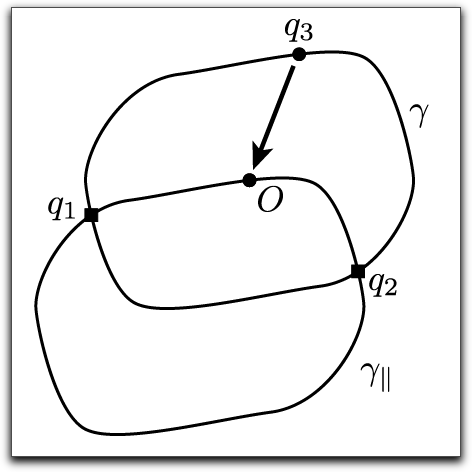
Fig. 1: Example for a origin symmetric convex curve.
If the curve is a circle, every one knows very well this theorem is true.
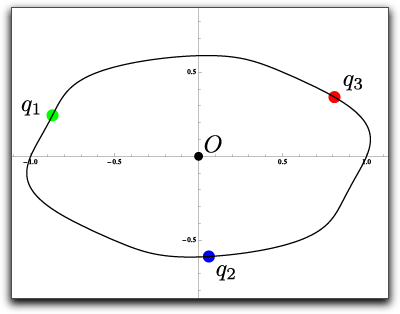
The following theorems give us a method to find these points.
Read our paper J. Phys. A: Math. Theor. 42 395205 (16pp) 2009 doi: 10.1088/1751-8113/42/39/395205 or arXiv http://arxiv.org/abs/0906.2249 for more generic theorem.

Fig. 1: Example for a origin symmetric convex curve.
If the curve is a circle, every one knows very well this theorem is true.
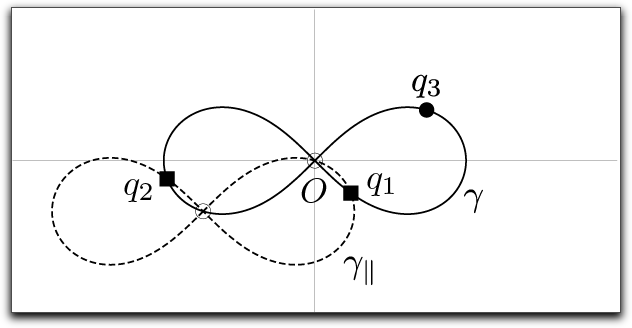
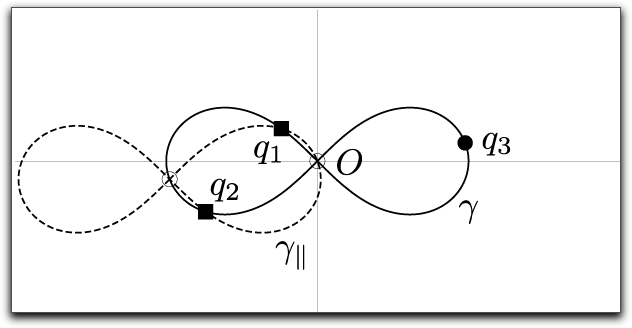
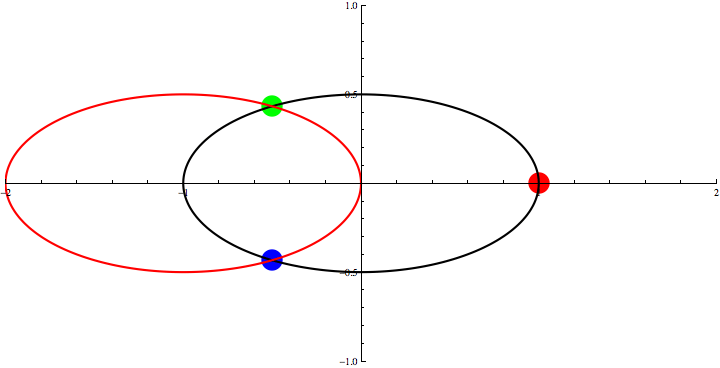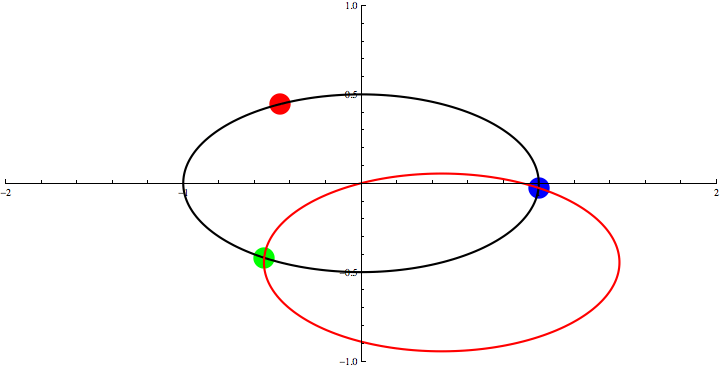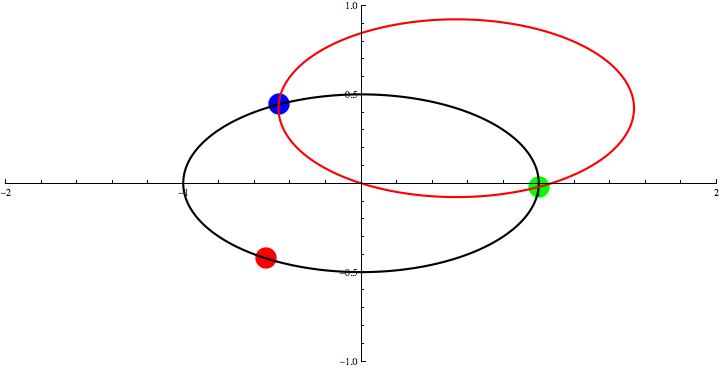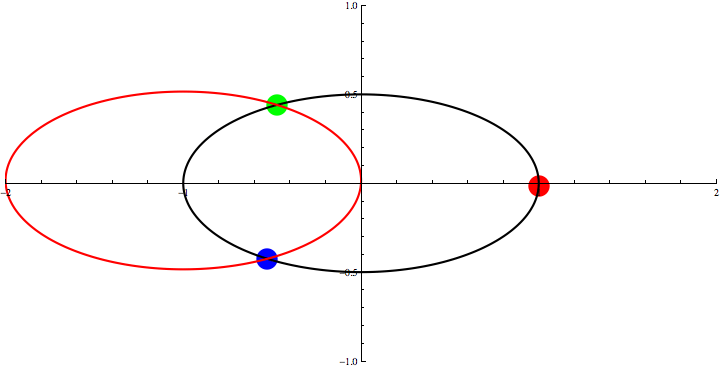
Fig. 2: Example for a eight-shaped curve.
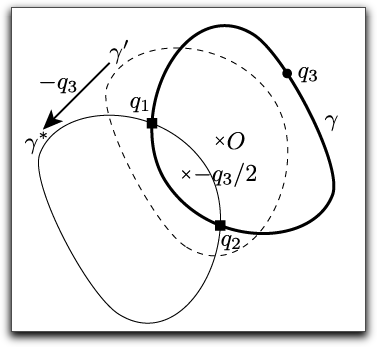
Fig. 3: Example for a general convex curve.
The curve γ* is the image of γ by the inversion
with respect to the point −q3/2.
Alternatively,
the curve γ* can be made by the following two steps.
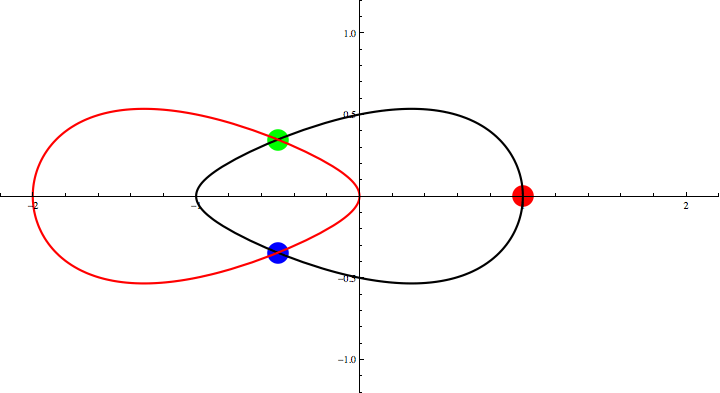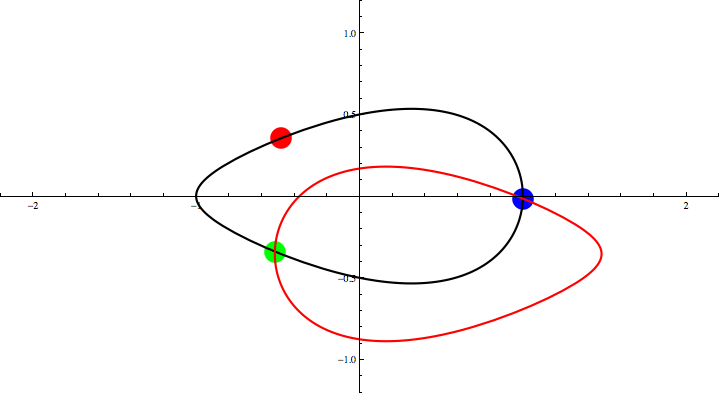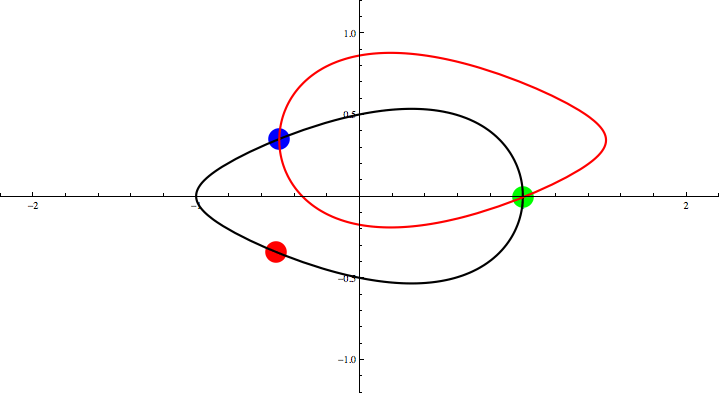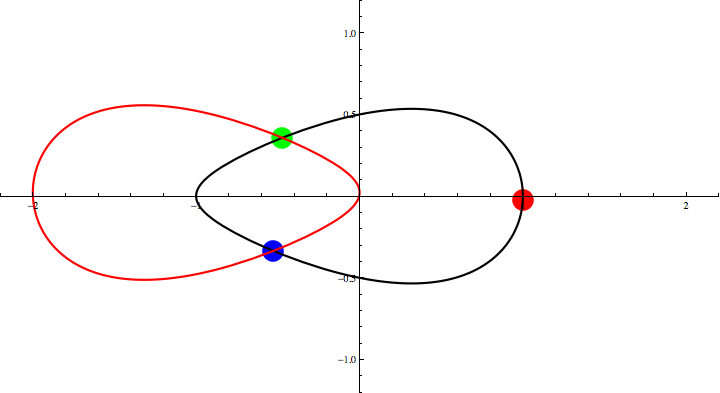
Animation 1: Three Points Theorem for the figure-eight solution.
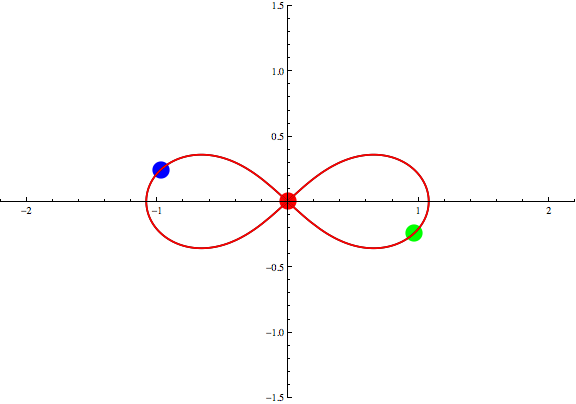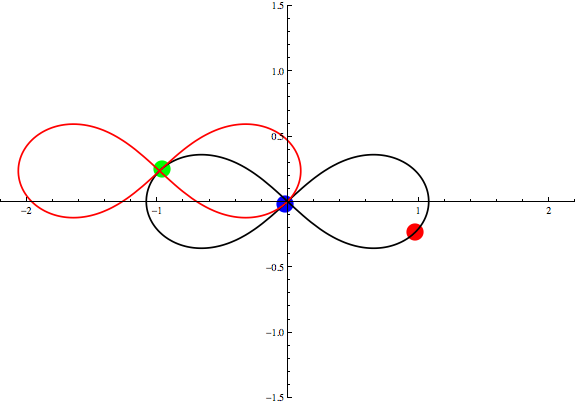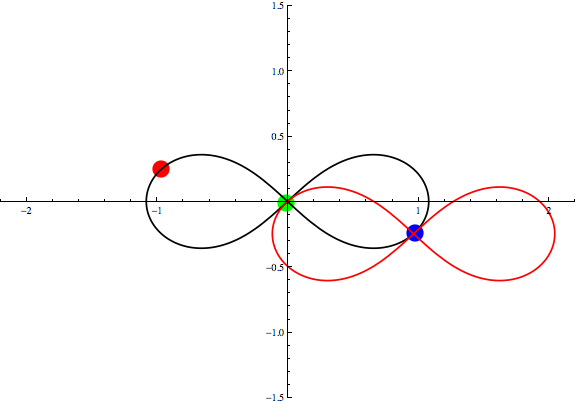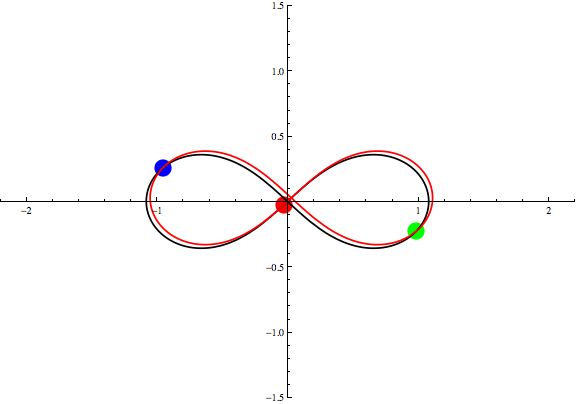
The red, green and blue circles represent
three bodies for the figure-eight solution
found by Moore, Chenciner and Montgomery
under the Newtonian gravity.
The black eight-shaped curve is the orbit for the solution.
We take the red circle for q3,
then the positions for other two points that satisfy
q1+q2+q3=0
is given by the cross points of the original eight (black curve)
and its parallel translation (red curve).
Animation 2: Three Points Theorem for an oval.
Animation 3: Three Points Theorem for an egg-shaped curve.
Animation 4: Three Points Theorem for a distorted curve.