Centers for the Figure-Eight Solution under 1/r^2 Potential

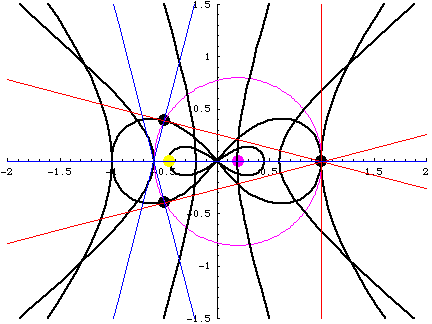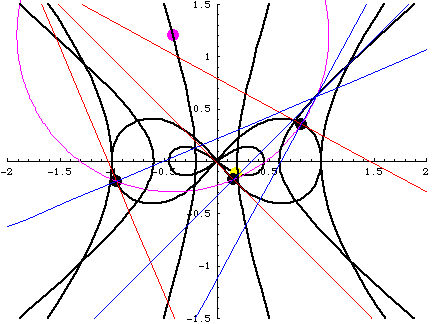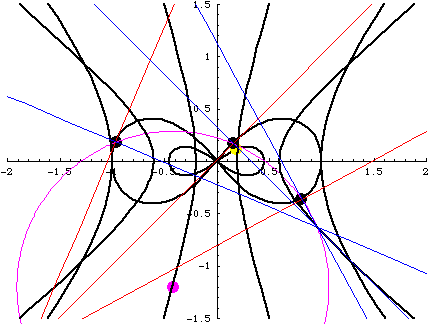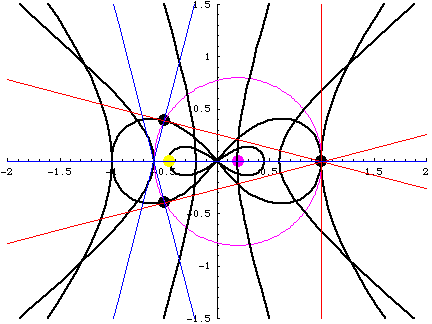
Three tangent lines meet at the "Center of Tangents" $C_t(t)$.
Three normal lines meet at the "Center of Normals" $C_n(t)$.
The points $C_t$ and $C_n$ are the end points of a diameter
of the circumcircle of the triangle made by three masses.
This is due to the fact $L=0, I=constant$.

• Large eight: The figure-eight orbit.
  • Black points: The position of masses $q_i(t)$.
  • Red lines: Tangent lines. They meet at $C_t(t)$.
  • Blue lines: Normal lines. They meet at $C_n(t)$.
• Purple moving circle: The circumcircle.
  • Purple point: The circumcenter.
• Hyperbola-like curves from inner to outer:
  • Orbit of the circumcenter.
  • Orbit of the "Center of Normals" $C_n(t)$.
  • Orbit of the "Center of Tangents" $C_t(t)$.
• Small eight: The orbit of the "Center of Force".
  • Yellow point: The "Center of Force".