See also Hiroshi Fukuda's site ``Three Body Problem'' http://kilin.clas.kitasato-u.ac.jp/3body/

Hiroshi Fukuda found many figure-eight solutions
under Lennard-Jones potentail
U=1/r^{12}-1/r^6.
The preprint
[1] H. Fukuda, T. Fujiwara and H. Ozaki,
Figure-eight choreographies of the equal mass three-body problem with Lennard-Jones-type potentials,
http://arxiv.org/abs/1606.08760
You can see many series for figure-eights in this paper.
The existence of figure-eight solutions under Lennard-Jones potential
was predicted by L. Sbano
in his talk at
SPT 2004 held at Cala Gonone, Italy.
He predicted that
``there are at least two solutions for sufficiently large period''.
[2] L. Sbano,
Symmetric solutions in molecular potentials,
Proceedings of the international conference SPT 2004,
World Scientific, 2005
[3] L. Sbano and J. Southall,
Periodic solutions of the N-body problem
with Lennard-Jones type potentials,
Warwick preprint, June 2007
[4] L. Sbano and J. Southall,
Periodic solutions of the N-body problem
with Lennard-Jones type potentials,
Dynamical Systems Vol. 25 #1, 2010
The followings are animations for some figure-eights that are found by Hiroshi Fukuda.
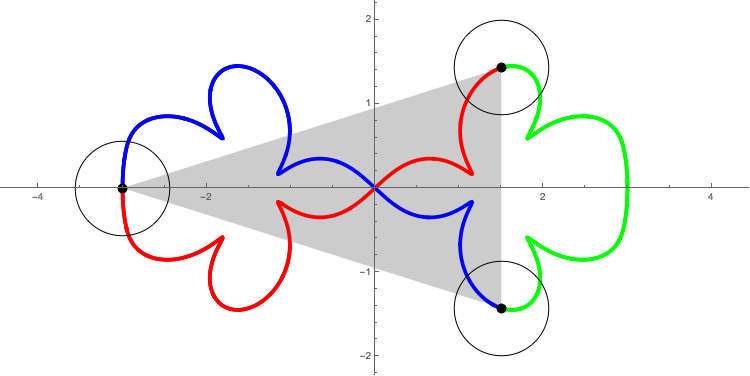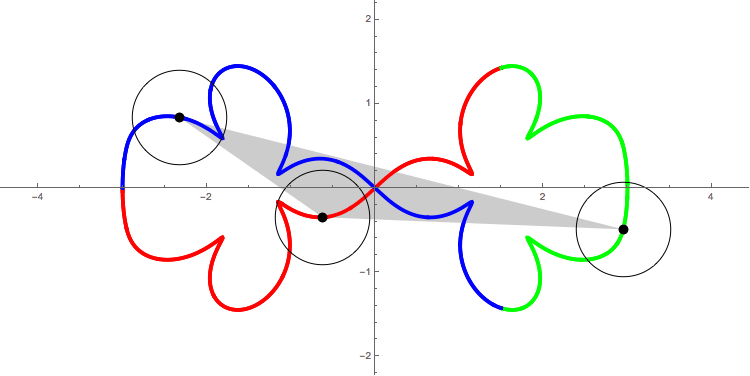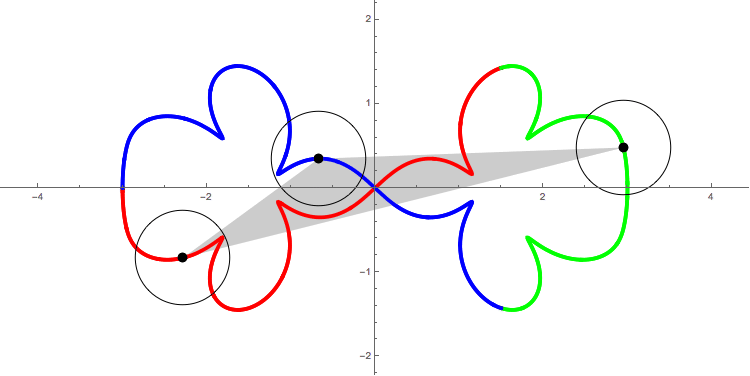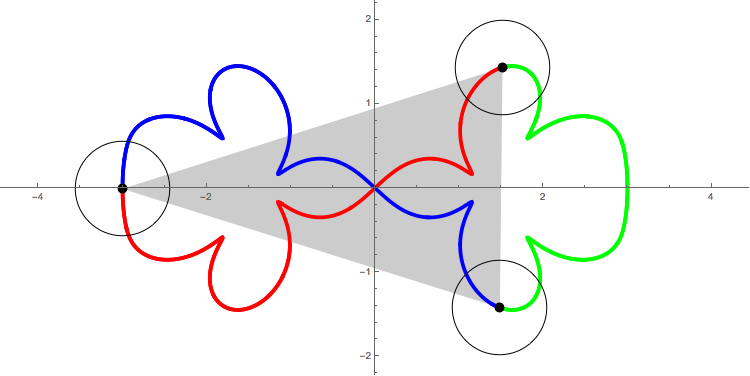
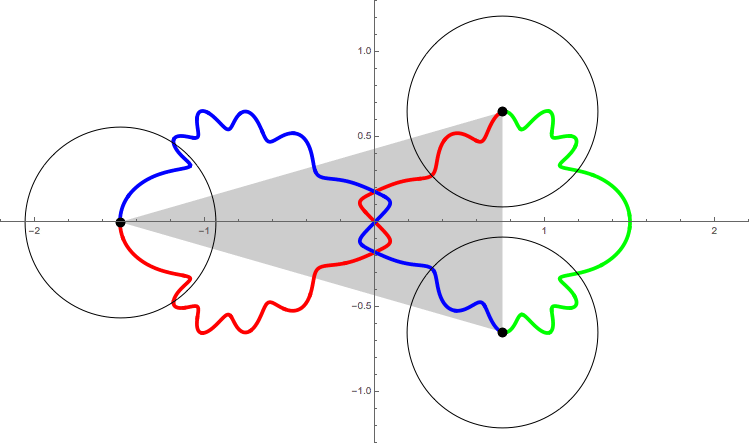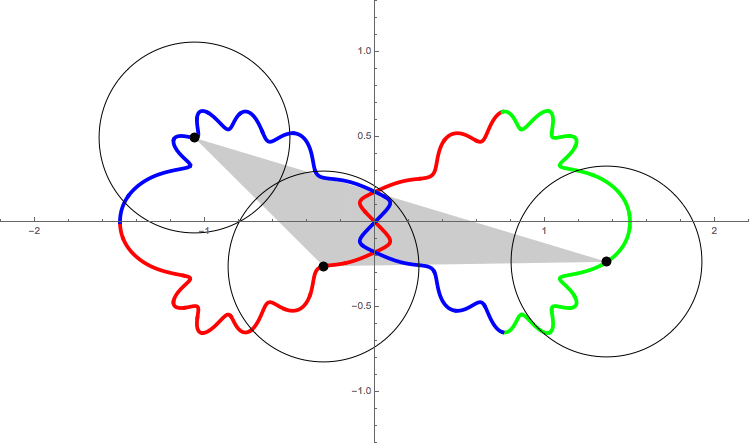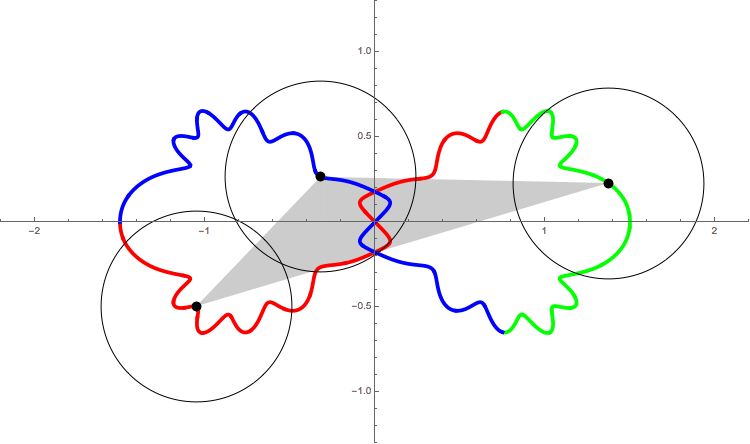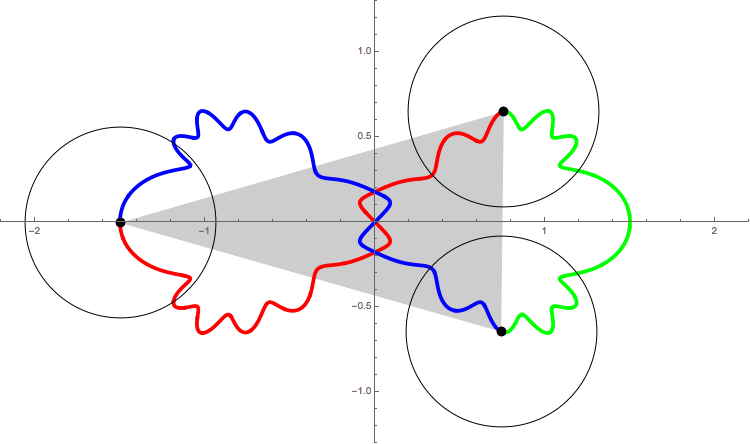
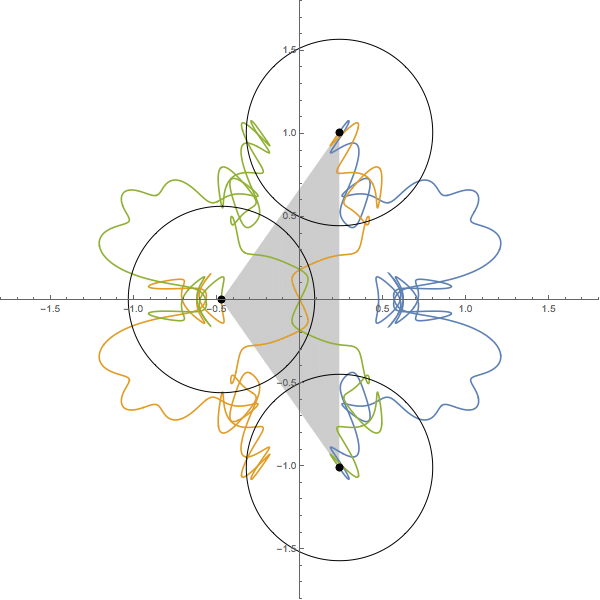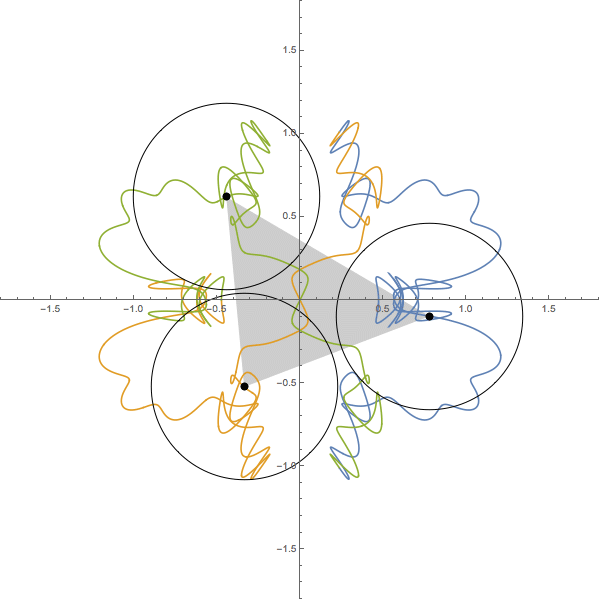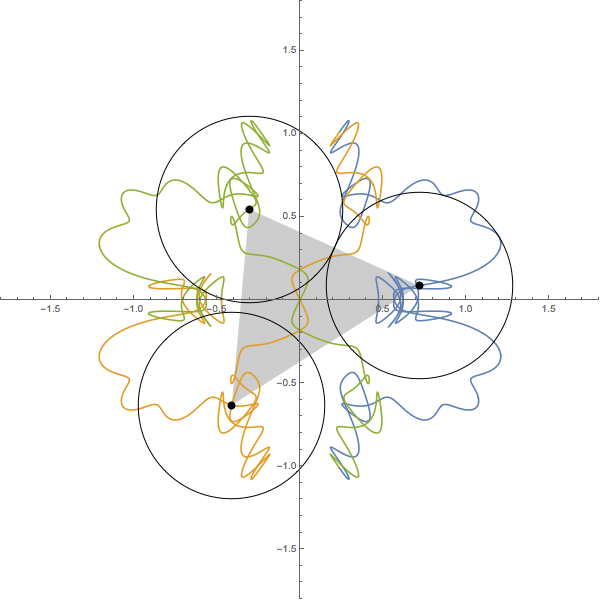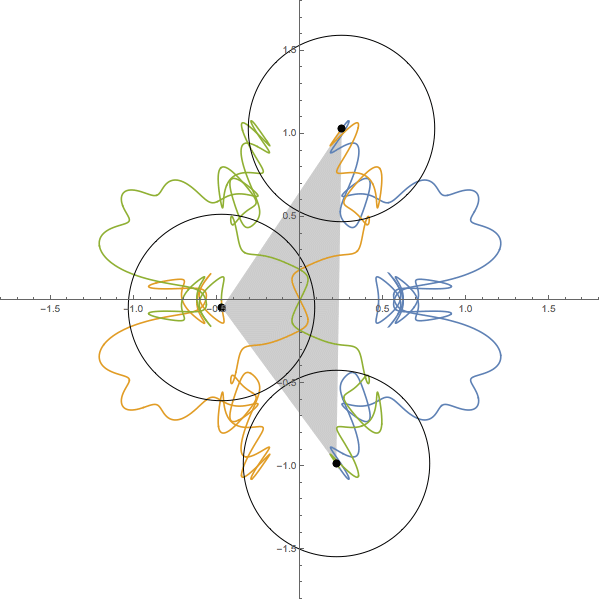
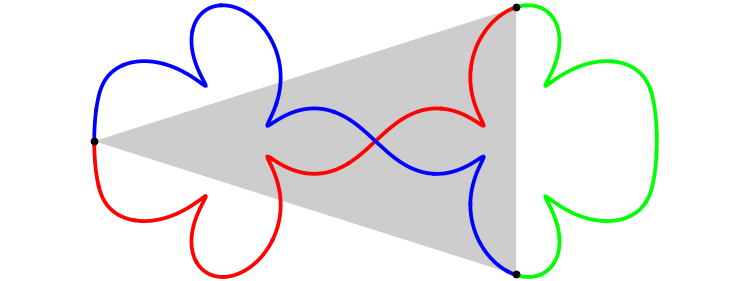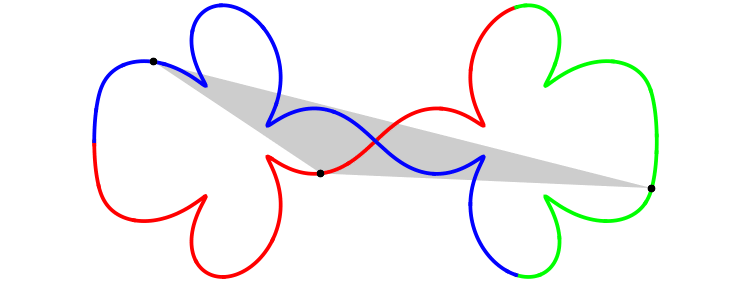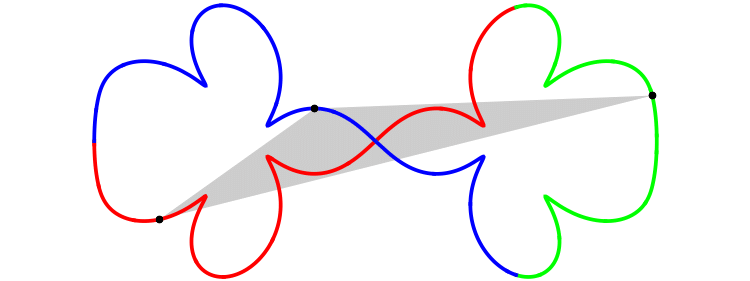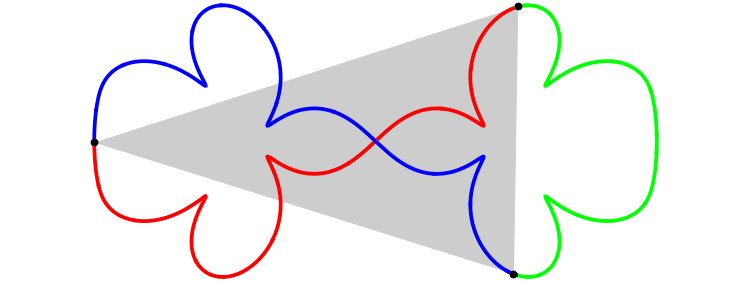
The following figure shows
the orbit of the figure-eight
of animation 3
in the ``shape plane'',
q_3(t)/(q_2(t)-q_1(t)).
If you need more precise picture, follow this link 20160703LennardJonesFig3Shape3.pdf
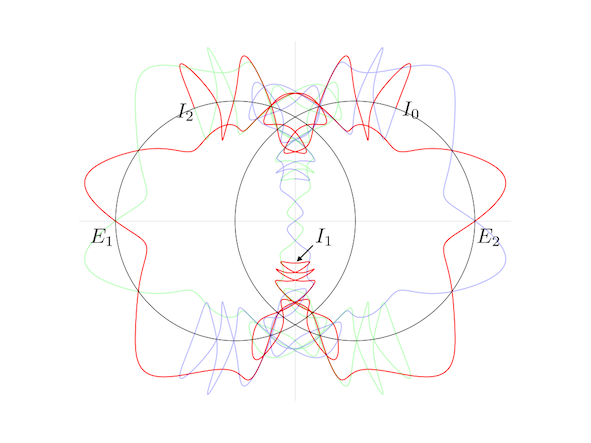
The X-axis is the equator of the ``shape sphere''. Any points on the equator represents colinear configuration. The Y-axis and two circles are the lines of longitude of the ``shape sphere'', whose mutual angle is equal to 2\pi/6. Any point on these five longitude lines represents isosceles configuration.
The red curve represents the interval of time [0, T/3]. And green and blue one represent [T/3, 2T/3] and [2T/3, T] respectively.
See the red curve.
At t=0, the motion starts at the isosceles configuration I_0.
At t=T/12, it passes through the Euler point E_1.
Then at 2T/12, I_1.
Namely,
in short expression,
I_0(t=0) --> E_1(T/12) -->I_1(2T/12) --> E_2(3T/12) --> I_2(4T/12=T/3)
In the interval of time [0, T/3], the motion passes through just two Euler points E_1 and E_2. For isosceles configurations, although the motion passes through many isosceles configurations, only pathes at I_0, I_1 and I_2 are parpendiculer to the longitude line. This is the requirement for the figure-eight solution. So, this solution has a qualification to be called ``one of the figure-eight solution''.