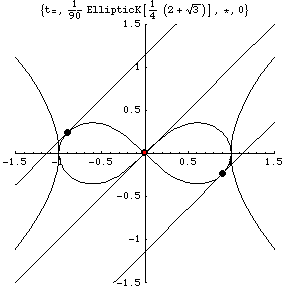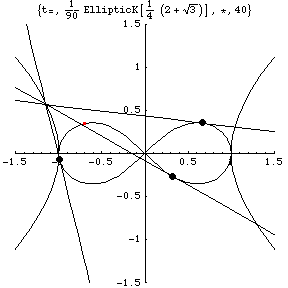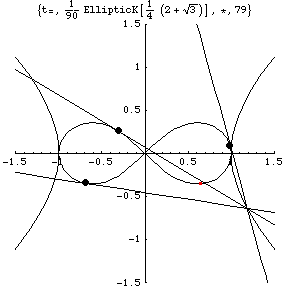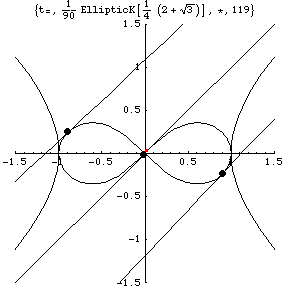
Three tangent lines from the three bodies meet
at a point on the rectangular hyperbola
That is, let c be the cross point, then the red circle represents c'=c/(c^2).
The red point c' is also on the lemniscate.
(The red point c' looks as if it were on a tangent line. But this is not true. It is on the line which connects c and the origin.)
Three bodies(black circles) and c' (red circle) are always in the different quadrant each other. Because (i)this is true at a instant, (ii)when the c' passes through the origin, one body passes through the same point in the opposite direction and (iii)when the c' passes through the horizontal line, one body passes through the same point in the opposite direction.
The cross point c and the inversion c' are always in the same quadrant. Therefore, three bodies(black circles) and the cross point c are always in the different quadrant each other.