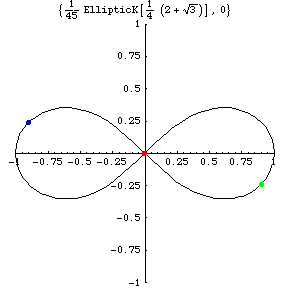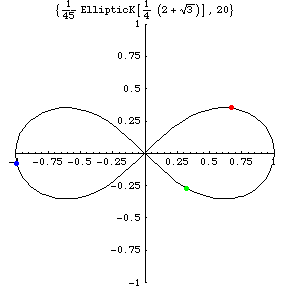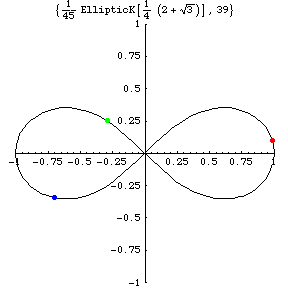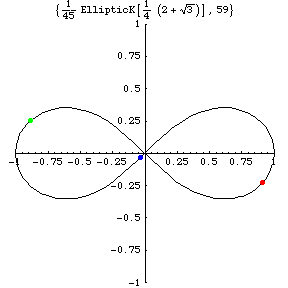
x(t)=(x(t),y(t))
v(t)=d/dtx(t)=(v_{x}(t),v_{y}(t))
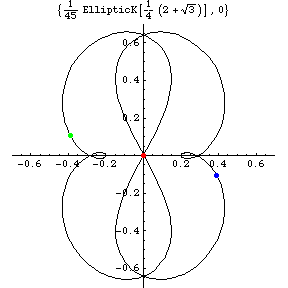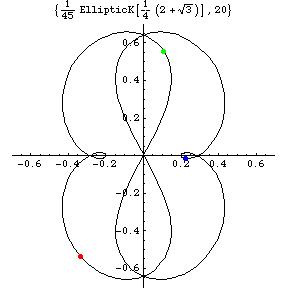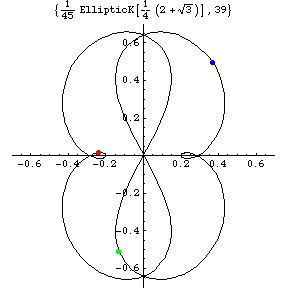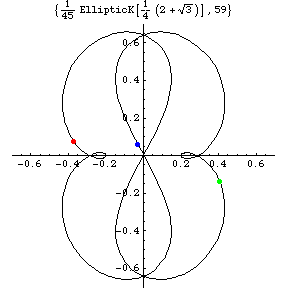
a(t)=d^2/dt^2x(t)=(a_{x}(t),a_{y}(t))
 x(t)=(x(t),y(t)) |
 v(t)=d/dtx(t)=(v_{x}(t),v_{y}(t)) |
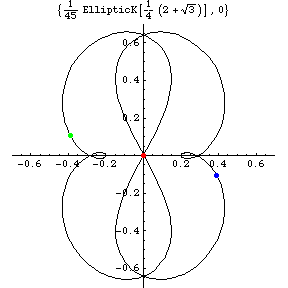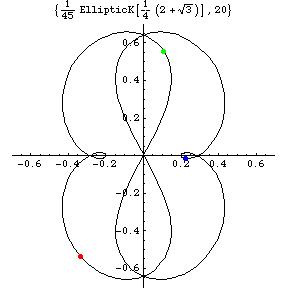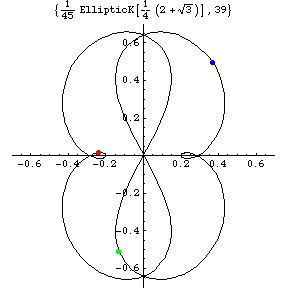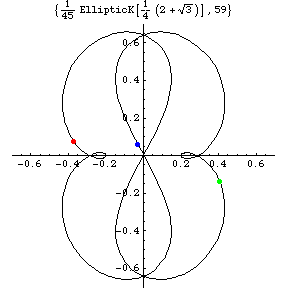 a(t)=d^2/dt^2x(t)=(a_{x}(t),a_{y}(t)) |
WRONG:
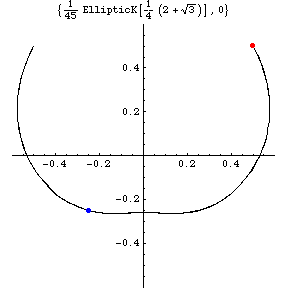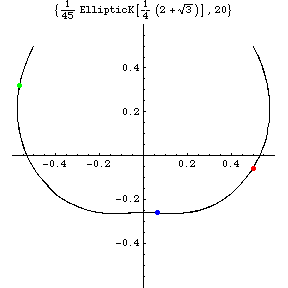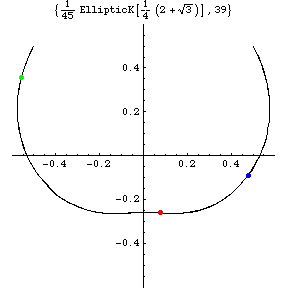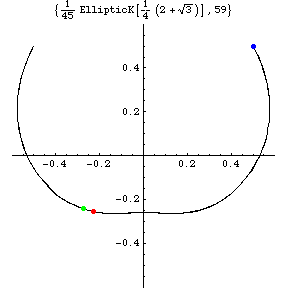
But the above figure for the acceleration a(t) shows
small but obvious difference between Sim\'{o}'s and ours.
That is, our solution has two small loops near
a=( \mp 3(2-sqrt{3})/4,0) = (\mp 0.20096...,0),
which correspond to near x=(\pm 1,0).
We believe the Sim\'{o}'s solution has no loops near these points.
Instead of small loop, the Sim\'{o}'s solution has cusp in a(t) plane
at these points.
CORRECT:
Acceleration curve has two small loops for
Figure-Eight under the potential
U= \alpha^{-1} \sum_{i < j} r_{ij}^{\alpha}
with \alpha < -1+ \epsilon.
Where 0 < \epsilon < 1.
Therefore, there are small loops in the acceleration space
for the the Figure-Eight solution
under the Newton potential (-1/r_{ij})
or -1/r_{ij}^2 potential.
On the other hand, there are no small loops under the \log potential.
The existence of the small loops in the acceleration space
means that
y \ddot{y} is not always negative.
Consider a short time interval after the blue or red mass
pass through the X-axes
in real space (the left most fig.).
The acceleration in Y-direction is negative
for this very short time interval.
(In other words, y \ddot{y} > 0 in this short time interval.)
Then, the acceleration in Y-direction become posuitive
as it looks like. ( y \ddot{y} < 0 )
(Corrected 1/29/2004)