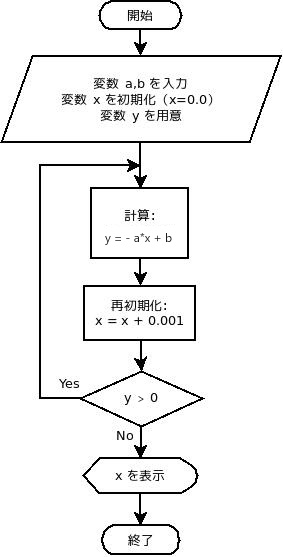
1からxまでの和を求めるプログラムを作ってみましょう.
プログラムの構造は,次のようになります.
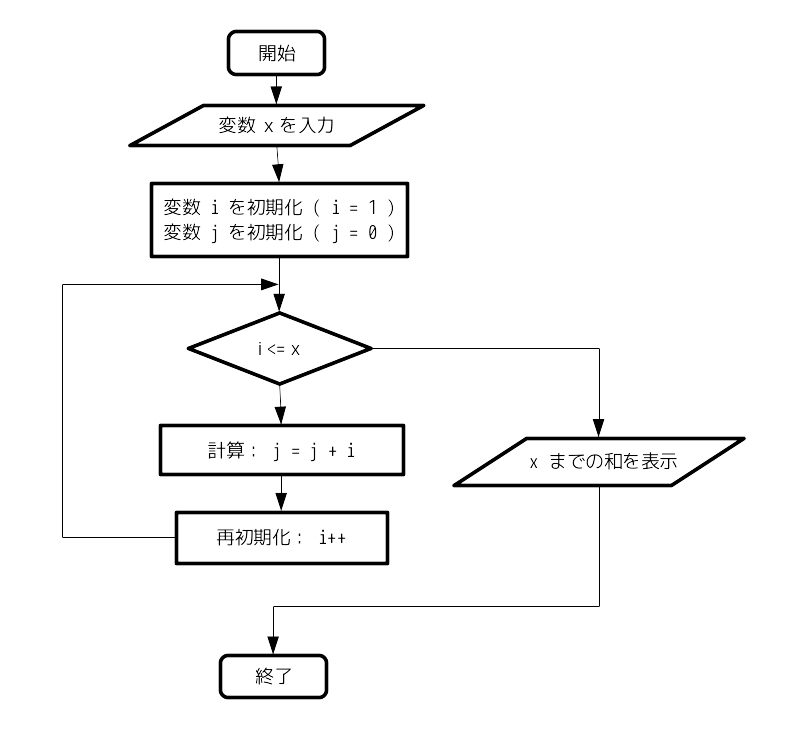
各段階での変数の中身を見てみましょう.
例えば,5を入力したとします( x = 5 となる).
| j | i | x | ||
|---|---|---|---|---|
| 初期化 | 0 | 1 | 5 | |
| ループ部分:(while の中身) | ||||
| ループ回数(iの値) | j=j+i | 内容 | i++(再初期化) | 条件判定(i < = x) |
| 1 | 1=0+1 | 1=0+1 | i++ = 2 | 2 < = 5 : true |
| 2 | 3=1+2 | 3=(0+1)+2 | i++ = 3 | 3 < = 5 : true |
| 3 | 6=3+3 | 6=(0+1+2)+3 | i++ = 4 | 4 < = 5 : true |
| 4 | 10=6+4 | 10=(0+1+2+3)+4 | i++ = 5 | 5 < = 5 : true |
| 5 | 15=10+5 | 15=(0+1+2+3+4)+5 | i++ = 6 | 6 < = 5 : false |
| 終了時 | ||||
| 15 | 15 : 5までの和 | 6 | ||
以上のように,i を1づつ増やしながら計算させ,while の条件を i<=x とすれば,入力した回数だけ繰り返し計算することになる.その結果,最終的に j に入力した数値の和が入ることになる.
具体的には次のように書きます.
/**************************************************
反復構造:while文
**************************************************/
import javafx.application.Application;
import javafx.geometry.Insets;
import javafx.geometry.Pos;
import javafx.stage.Stage;
import javafx.scene.Scene;
import javafx.scene.layout.VBox;
import javafx.scene.control.Label;
import javafx.scene.control.TextField;
import javafx.scene.layout.HBox;
public class FirstREP extends Application{
public static void main(String[] args) {
launch(args);
}
TextField tf1 = new TextField();
Label label1 = new Label("整数を入力して下さい");
Label label2 = new Label();
@Override
public void start(Stage stage) throws Exception {
stage.setTitle("Application FirstREP");
VBox root = new VBox();
root.setAlignment(Pos.CENTER);
root.setPadding(new Insets(10,10,10,10));
root.setSpacing(10.0);
HBox pane1 = new HBox();
pane1.setAlignment(Pos.CENTER);
pane1.setPadding(new Insets(10,10,10,10));
pane1.setSpacing(5.0);
tf1.setAlignment(Pos.CENTER_RIGHT);
tf1.setMaxWidth(50);
pane1.getChildren().addAll(label1,tf1);
tf1.setOnAction(event -> calcValue());
root.getChildren().addAll(pane1,label2);
Scene scene = new Scene(root,400,200);
stage.setScene(scene);
stage.show();
}
private void calcValue() {
String s = tf1.getText();
int x = Integer.parseInt(s);
//while文
//初期化
int i = 1;
int j = 0;
while(i <= x){ // i <= x が条件式
j = j+i; //繰り返す処理
i++; //再初期化 ( i = i + 1 と書いても同じ)
}
label2.setText( x + "までの和は" + j + "です.");
}
}